Selection Sort
The idea of selection sort is rather simple: we repeatedly find the next largest (or smallest) element in the array and move it to its final position in the sorted array. Assume that we wish to sort the array in increasing order, i.e. the smallest element at the beginning of the array and the largest element at the end. We begin by selecting the largest element and moving it to the highest index position. We can do this by swapping the element at the highest index and the largest element. We then reduce the effective size of the array by one element and repeat the process on the smaller (sub)array. The process stops when the effective size of the array becomes 1 (an array of 1 element is already sorted).For example, consider the following array, shown with array elements in sequence separated by commas:
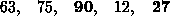
The leftmost element is at index zero, and the rightmost element is at the highest array index, in our case, 4 (the effective size of our array is 5). The largest element in this effective array (index 0-4) is at index 2. We have shown the largest element and the one at the highest index in bold. We then swap the element at index 2 with that at index 4. The result is:
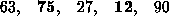
We reduce the effective size of the array to 4, making the highest index in the effective array now 3. The largest element in this effective array (index 0-3) is at index 1, so we swap elements at index 1 and 3 (in bold):

The next two steps give us:
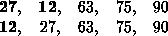
Bubble Sort
An alternate way of putting the largest element at the highest index in the array uses an algorithm called bubble sort. While this method is neither as efficient, nor as straightforward, as selection sort, it is popularly used to illustrate sorting. We include it here as an alternate method.Like selection sort, the idea of bubble sort is to repeatedly move the largest element to the highest index position of the array. As in selection sort, each iteration reduces the effective size of the array. The two algorithms differ in how this is done. Rather than search the entire effective array to find the largest element, bubble sort focuses on successive adjacent pairs of elements in the array, compares them, and either swaps them or not. In either case, after such a step, the larger of the two elements will be in the higher index position. The focus then moves to the next higher position, and the process is repeated. When the focus reaches the end of the effective array, the largest element will have ``bubbled'' from whatever its original position to the highest index position in the effective array.
For example, consider the array:

In the first step, the focus is on the first two elements (in bold) which are compared and swapped, if necessary. In this case, since the element at index 1 is larger than the one at index 0, no swap takes place.
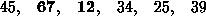
Then the focus move to the elements at index 1 and 2 which are compared and swapped, if necessary. In our example, 67 is larger than 12 so the two elements are swapped. The result is that the largest of the first three elements is now at index 2.
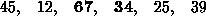
The process is repeated until the focus moves to the end of the array, at which point the largest of all the elements ends up at the highest possible index. The remaining steps and result are:

Insertion Sort
The two sorting algorithms we have looked at so far are useful when all of the data is already present in an array, and we wish to rearrange it into sorted order. However, if we are reading the data into an array one element at a time, we can take another approach - insert each element into its sorted position in the array as we read it. In this way, we can keep the array in sorted form at all times. This algorithm is called insertion sort.
With this idea in mind, Let us see how the algorithm would work. If the array is empty, the first element read is placed at index zero, and the array of one element is sorted. For example, if the first element read is 23, then the array is:
23, ?
We will use the symbol, ?, to indicate that the rest of the array elements contain garbage. Once the array is partially filled, each element is inserted in the correct sorted position. As each element is read, the array is traversed sequentially to find the correct index location where the new element should be placed. If the position is at the end of the partially filled array, the element is merely placed at the required location. Thus, if the next element read is 35, then the array becomes:23, 35, ?
However, if the correct index for the element is somewhere other than at the end, all elements with equal or greater index must be moved over by one position to a higher index. Thus, suppose the next element read is 12. The correct index for this element in the current array is zero. Each element with index zero or greater in the current partial array must be moved by one to the next higher position. To shift the elements, we must first move the last element to its (unused) higher index position, then, the one next to the last, and so on. Each time we move an element we leave a ``hole'' so we can move of the adjoining element, and so on. Thus, the sequence of moving elements for our example is:23, 35, ?, ?
23, ?, 35, ?
?, 23, 35, ?
The index zero is now vacant, and the new element, 12, can be put in that position.12, 23, 35, ?
The process repeats with each element read in until the end of input. So, if the next element is 47, we would traverse from the beginning of the array until we find larger than 47 or until we reach the end of the filled part of the array. In this case, we reach the end of the array, and insert 47:12, 23, 35, 47, ?Shell Sort
Shellsort is one of the oldest sorting algorithms, named after its inventor D.L. Shell (1959) [Sh]. It is fast, easy to understand and easy to implement. However, its complexity analysis is a little more sophisticated. Idea The idea of Shellsort is the following: arrange the data sequence in a two-dimensional array sort the columns of the array The effect is that the data sequence is partially sorted.
The process above is repeated, but each time with a narrower array, i.e. with a smaller number of columns. In the last step, the array consists of only one column.
In each step, the sortedness of the sequence is increased, until in the last step it is completely sorted. However, the number of sorting operations necessary in each step is limited, due to the presortedness of the sequence obtained in the preceding steps.
Example:
Let 3 7 9 0 5 1 6 8 4 2 0 6 1 5 7 3 4 9 8 2 be the data sequence to be sorted. First, it is arranged in an array with 7 columns (left), then the columns are sorted (right):
|
|
Data elements 8 and 9 have now already come to the end of the sequence, but a small element (2) is also still there. In the next step, the sequence is arranged in 3 columns, which are again sorted:
|
|
Now the sequence is almost completely sorted. When arranging it in one column in the last step, it is only a 6, an 8 and a 9 that have to move a little bit to their correct position.
Implementation
Actually, the data sequence is not arranged in a two-dimensional array, but held in a one-dimensional array that is indexed appropriately. For instance, data elements at positions 0, 5, 10, 15 etc. would form the first column of an array with 5 columns.
The "columns" obtained by indexing in this way are sorted with Insertion Sort, since this method has a good performance with presorted sequences.
The following program sorts an array a from index position 0 through n-1. The number of columns used for arranging data in each step is in array cols. Thus, data are arranged in 1391376 columns in the first step and in one column in the last step. (Note that essentially nothing is done if the number of columns h is larger than the number of data elements n.) Each column is sorted by Insertion Sort. First, data of the second row (beginning at i = h) are sorted to the correct position in their column, then data of the third row (when i reaches value 2h) etc.
References:






